Determining the Strength of 3D Resins: A Study on Compression Testing

Introduction

Testing the strength of a 3D resin is essential to determine its quality and suitability for various applications. The strength of 3D resin can be determined through several mechanical tests, including tensile testing, compression testing, and impact testing. These tests can help determine the maximum load the resin can withstand and its overall durability.

• Tensile Testing. Tensile testing is a standard method used to measure the strength of 3D resin. In this test, a resin sample is placed in a tensile testing machine and gradually pulled apart. The maximum load at which the resin breaks is recorded and used to calculate its tensile strength.
• Compression Testing. Compression testing measures the strength of 3D resin when subjected to a compressive load. In this test, a resin sample is placed in a compression testing machine and subjected to increasing loads until it fails. The maximum load at which the resin fails is recorded and used to calculate its compressive strength.
• Impact Testing. Impact testing measures the ability of a 3D resin to withstand sudden impact loads. In this test, a resin sample is subjected to a sudden impact, and the amount of energy it absorbs is measured. This test helps determine the overall durability of the resin and its ability to withstand shocks and vibrations.

In this study, we set standard compression testing for 3D resins. We will describe the equipment, setup, and testing procedure. As an example, we will also compare the strength of AnyCubic ABS+ resin and ABS Pro resin. We want to describe a method that can tell “good resin” from “bad resin”.

Study Setup

Mechanical

We used an HP-500N Digital Force Gauge. It comes with four compression test parts, and one tensile test part.

Gauge Parameters -

• Capacity: 500N/110lbf/50Kgf
• Resolution: 0.1N/0.01lbf/0.01Kgf
• Accuracy: ±0.5%

Test Stand Parameters:

• Model: HLD Wheel-Operated Test Stand
• Stroke: 180mm/7.0in.
• Mounting hole: 4-M3 (30145mm), 4-M4 (4090mm)
• Maximum load: 1000N/100kg.

We have made modifications to the test stand. For compression tests, we utilized the included cylindrical, pointed metal head on top. We designed a base with a central hole for the compression head to pass through and a square platform to securely hold the test piece.

The test pieces are 20 mm x 20 mm x 1 mm squares that are printed vertically. Printing them horizontally could result in the bed level affecting the thickness of the piece.

Measurement

The number of samples to take in a study depends on several factors, including variance measurement. Variance is a measure of the spread or dispersion of the data. The larger the variance, the greater the variability in the data, and the larger the sample size needed to get a reliable estimate of the population mean. On the other hand, if the variance is small, a smaller sample size may be sufficient.

One commonly used method to determine the sample size based on variance is the sample size calculation formula, which takes into account the population variance, desired level of precision, and desired level of confidence. The formula for sample size calculation is given:

n = (Z^2 * σ^2) / (E^2)

where:

• n is the sample size
• Z is the Z-score associated with the desired level of confidence (e.g., Z=1.96 for 95% confidence)
• σ^2 is the population variance
• E is the desired level of precision (e.g., 0.05 for 5%)

This formula gives the minimum sample size needed to achieve the desired level of accuracy and confidence. In practice, a larger sample size may account for any sampling variability or measurement errors.

In this example, we used the sample size calculation formula to determine the minimum sample size needed to achieve the desired level of precision and confidence. The larger the variance, the larger the sample size required, and vice versa. Using the formula, we can ensure that the sample size is adequate for our needs and that the study results are reliable.

In conclusion, the number of samples to take in a study depends on the measurement of variance, the desired level of precision and confidence, and the study's goals. The sample size calculation formula can be used to estimate the minimum sample size needed to achieve the desired level of precision and confidence. Still, a larger sample size may account for sampling variability or measurement errors.

Result

Curing Time on Variance and Sample Size

Variance increases after curing: We did some preliminary testing and found at a curing time of 10 minutes, we need to collect nearly 30 samples. Therefore, we tested variance against different curing times and found no curing has the smallest variance.

We want to measure the compression of resin with a 95% confidence level and a precision of ± 5 kgf. The Z value is 1.96 for 95% and 1.65 for 90%. We collected 40 samples from non-curing resin and 10-minute cured resin. For example, the measured mean of 10-min cured resin is 77.93, and the variance is 195.01.

Using the formula, we can calculate the minimum sample size as follows:

n = (Z^2 * σ^2) / (E^2)

where:

• Z = 1.96 (for 95% confidence level)
• σ^2 = 195.01 (population variance)
• E = 5 (desired precision)

Substituting these values into the formula, we get:

n = (1.96^2 * 195.01) / (5^2) = 29.96

Since the sample size must be a whole number, we round up to the nearest number, 30. Therefore, we need to take a sample of at least 30 apples to estimate the mean compression of the resin with a 95% confidence level and a precision of ± 5 kgf, and we only need to take 5 samples if we do not cure the resin (see Table 1).

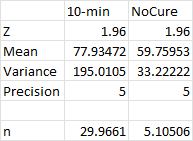
Table 1. Estimated sample number for cured (10 min) and not cured resin

As a result, we have decided to gather 30 samples of cured resin and 10 samples of uncured resin. In future studies, we aim to address questions such as 1) What causes the variance increase in cured resin? and 2) Can the variance be attributed to the piece's position on the curing station?

Compare resin strength between two kinds of resins

 Therefore, we took 80 samples from two resins: 

Group #1. AnyCubic ABS-Like Resin +	Group #2 AnyCubic ABS-Like Pro
Price: Click here	Price: Click here
Manufacture claim: excellent tensile and bending strength as well as hardness and toughness. It has past extensive testing and can perform under a normal tensile force and compressive stress.	Manufacture claim: ABS-like resin Pro is designed to have a respectively 52% and 60% increase in tensile strength and bending strength compared to standard resins

The result can be seen from the following box chart.

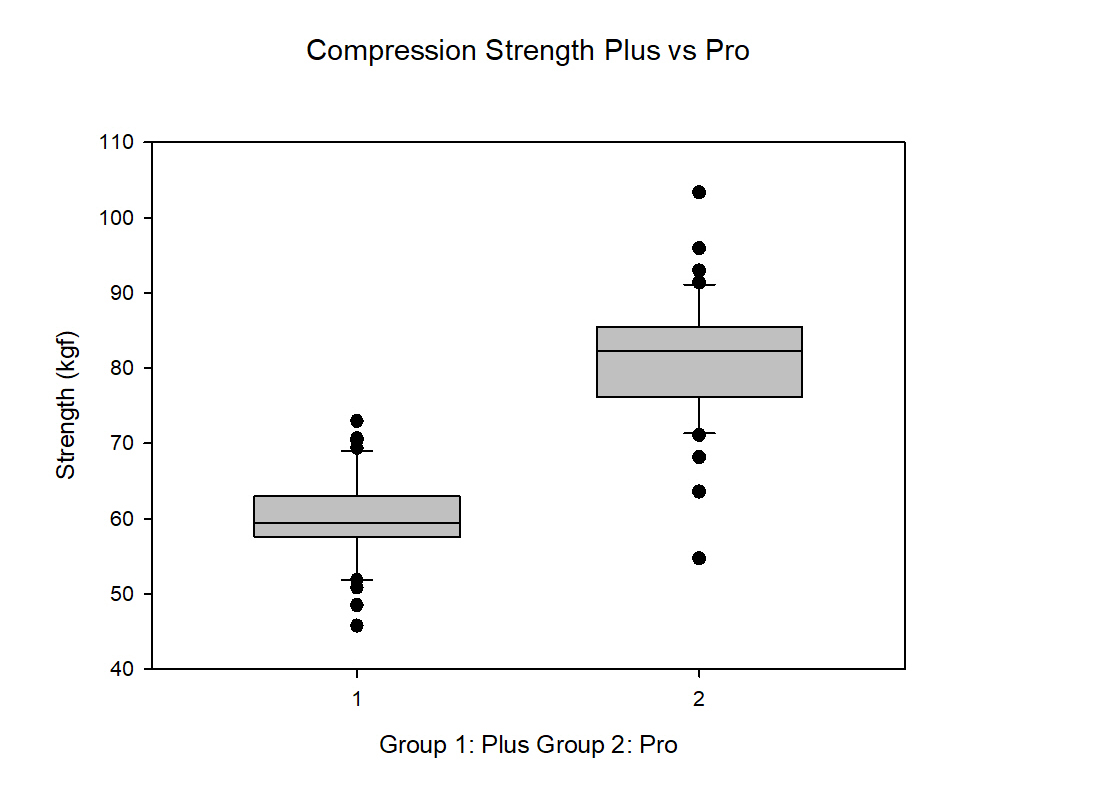
A box plot, also known as a box-and-whisker plot, is a graphical representation of the distribution of numerical data. It provides an overview of the median, quartiles, and outliers in the data.

To read a box plot with variance, mean, and outliers, follow these steps:

1. The box represents the middle 50% of the data, known as the interquartile range (IQR). The box starts at the first quartile (25th percentile) and extends to the third quartile (75th percentile). A line inside the box indicates the median (50th percentile). Here we can see that group #2 (Pro) has a higher median than group #1.
2. The "whiskers" represent the range of the data, excluding outliers. They extend from either side of the box to the minimum and maximum values unless there are outliers.
3. Outliers are plotted individually as dots beyond the whiskers. Outliers are data points that lie more than 1.5 times the IQR from the lower and upper quartiles. We can see group #2’s outliers are more spread than group #1.

The box plot provides a quick and easy way to see the data distribution and identify any outliers, while the mean and variance give a better understanding of the central tendency and spread of the data.

Group #2 has a higher mean and median than #1. We decide to conduct a statistical test to tell if the two groups are significant differences. We first tested if they were following normal distribution, and they were not (P<0.05). Therefore, we didn’t conduct a T-test. We used Mann-Whitney Rand Sum Test instead.

Table: Results from Mann-Whitney Rank Sum Test

Group        N         Missing         Median           25%             75%           

Plus        40        0        59.398        57.556        62.787        

Pro        40        0        82.230        76.328        85.424        

Mann-Whitney U Statistic= 47.000

T = 867.000  n(small)= 40  n(big)= 40  (P = <0.001)

The difference in the median values between the two groups is greater than would be expected by chance; there is a statistically significant difference  (P = <0.001)

Therefore, we conclude that AnyCubic ABS Like Pro is better (about 40% of a performance boost) than AnyCubic ABS Like Plus. It is important to note that these tests are performed on standardized resin samples, and the results may vary depending on the model's size, shape, and orientation. Additionally, these tests are typically performed at room temperature. They do not consider the effects of environmental factors, such as temperature and humidity, on the strength of the resin.

In conclusion, the strength of a 3D resin can be determined through various mechanical tests, including tensile testing, compression testing, and impact testing. These tests can provide valuable information about the quality and suitability of the resin for various applications. However, it is essential to consider the limitations of these tests and perform additional tests as needed to ensure that the resin meets the specific requirements of a particular application.