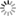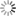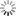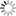
Parametric Art - Fusion of Chaos Fractal Art in Laser Engraving with Midjourney

This prompt describes the creation of a highly detailed, monochrome art piece using a parametric equation. The equation provides the basis for generating captivating art with various intricate patterns and textures. The two functions provided, x(t) and y(t), describe the x and y coordinates of points on a plane, with 'A', 'a', and 'b' being constants and 't' ranging from 0 to 2π. By experimenting with different values for these constants, the artist can create a wide range of unique designs.

The prompt also specifies the desired style of the artwork, which should resemble woodcut gravure, engraving, lino cut block print illustration. The piece should be in black and white and feature decorative details, textures, and a solid background. The artwork should be created from a wide-angle overhead view with even lighting, symmetrical composition, and a dream-like, thought-provoking atmosphere.

The piece should evoke a sense of movement, energy, innocence, and vulnerability while maintaining clean lines and sophisticated design elements. The final artwork should be highly detailed, of high quality, and have a sharp focus. The prompt also mentions the art should be in 4K resolution, resembling the Art Nouveau style, and be suitable for display at institutions such as MoMA.

Additionally, the prompt specifies that the artwork should be free from watermarks, copyrights, text, words, letters, or any elements that could be considered deformed, uninspired, or extraneous. The art should not include frames, borders, canvas, arches, hands, or people. The aspect ratio of the piece should be 3:2, and the viewer's vantage point should be from a distance of 5 units.

Prompt Base

A highly detailed [art] [subject]  drawn using a parametric equation, to create captivating art, x( t) = A* cos( a* t) * cost( t) + A* sin( b* t) * cost( t) and y( t) = A* cos( a* t) * sin( t) + A* sin( b* t) * sin( t) , where 'A', 'a' and 'b' are constants and 't' ranges from 0 to 2π. By experimenting with different values for '; A', 'a', and 'b', generate intricate woodcut gravure engraving lino cut block print illustration style, Monochrome black and white, decorative details, textures, isolated on solid background, wide angle overhead view, even lighting, symmetrical, dream - like, thought - provoking, clean lines, sophisticated, nature, movement, energy, innocence, vulnerability, intricate details, highly detailed, high quality, sharp focus, 4k, art nouveau, MoMA, illuminated --no watermark, copyright, text, words, letters, deformed, uninspired, frame, border, canvas, arch, hand, person –q 1 –ar 3:2 –v 5

• I suggest to heave [subject] empty, so the Midjourney can focus on generating a patter. Otherwise it will create a subject and wrap the pattern on the subject.
• [art] you can just leave it as "art" and let Midjourney does its stuff. Otherwise, try airbrush painting, line drawing, relief sculpture...
• The hands, person can be removed from "--no" list, and it will give a person to use the pattern rather than pattern itself
• For other parameters, such as "--tile", "--q", see Parameter list: https://docs.midjourney.com/docs/parameter-list

Example Prompt 

A highly detailed art drawn using a parametric equation, to create captivating art, x( t) = A* cos( a* t) * cost( t) + A* sin( b* t) * cost( t) and y( t) = A* c9s( a* t) * sin( t) + A* sin( b* t) * sin( t) , where 'A', 'a' and 'b' are constants and 't' ranges from 0 to 2π. By experimenting with different values for '; A', 'a', and 'b', generate intricate woodcut gravure engraving lino cut block print illustration style, Monochrome black and white, decorative details, textures, isolated on solid background, wide angle overhead view, even lighting, symmetrical, dream - like, thought - provoking, clean lines, sophisticated, nature, movement, energy, innocence, vulnerability, intricate details, highly detailed, high quality, sharp focus, 4k, art nouveau, MoMA, illuminated --no watermark, copyright, text, words, letters, deformed, uninspired, frame, border, canvas, arch, hand, person – q 1 –ar 3:2 –v 5

Result of the prompt:

Other Ready-to-Plugin Equations to Try:

Devil's Curve: 

The Devil's Curve is a quartic curve that resembles a cross or an X shape, with interesting properties and symmetries.

Equation: x(t) = t y(t) = t^3 - 3 * t

Parameters: t: The parameter that ranges from a specified negative value to a specified positive value, depending on the desired extent of the curve.

Nejibana (Twisted Petal) Curve

The Nejibana Curve is inspired by traditional Japanese art, resembling a twisting petal or a spinning top.

Equation: x(t) = (1 - 2 * cos(t) + sin(t)^2) * cos(t) y(t) = (1 - 2 * cos(t) + sin(t)^2) * sin(t)

Parameters: t: The parameter that ranges from 0 to 2π.

Polygonal Spiral

The Polygonal Spiral creates a pattern that resembles a polygon with rounded corners, spiraling outwards.

Equation: x(t) = (t^2 * cos(t)) / (t^2 + 1) y(t) = (t^2 * sin(t)) / (t^2 + 1)

Parameters: t: The parameter that ranges from a specified negative value to a specified positive value, depending on the desired extent of the spiral

Watt's Curve

Watt's Curve is a curve generated by a Watt's linkage, a mechanical linkage used in steam engines, creating a flowing, wavy shape.

Equation: x(t) = a * cos(t) + b * cos(a * t / b) y(t) = a * sin(t) - b * sin(a * t / b)

Parameters: a: The length of the first linkage in the mechanism. b: The length of the second linkage in the mechanism. t: The parameter that ranges from 0 to 2π.

Cornu Spiral (Euler Spiral Variation)

The Cornu Spiral is a variation of the Euler spiral that creates a more complex, twisting pattern.

Equation: x(t) = integral[0 to t] (cos(s^2) ds) y(t) = integral[0 to t] (sin(s^2) ds)

Parameters: t: The parameter that ranges from a specified negative value to a specified positive value, depending on the desired extent of the spiral.

Vary the parameters of each equation to create a diverse array of captivating designs in your parametric art.

Lissajous curve

Lissajous curve, which can create intricate patterns and designs. The Lissajous curve is defined by the following parametric equations:

x(t) = A * sin(a * t + δ) y(t) = B * sin(b * t)

Here, A and B are the amplitudes of the oscillations in the x and y directions, a and b are the frequencies of the oscillations, t is the parameter that ranges from 0 to 2π, and δ is the phase difference between the two oscillations.

By varying the values of A, B, a, b, and δ, you can create a multitude of captivating patterns and shapes in your artwork.

Epitrochoid Curve

Epitrochoid curve, which is a curve traced by a point attached to a circle rolling around the outside of another circle. The epitrochoid curve is defined by the following parametric equations:

x(t) = (R + r) * cos(t) - d * cos(((R + r) / r) * t) y(t) = (R + r) * sin(t) - d * sin(((R + r) / r) * t)

Here, R is the radius of the larger circle, r is the radius of the smaller circle, t is the parameter that ranges from 0 to 2π, and d is the distance between the center of the smaller circle and the point tracing the curve.

By experimenting with the values of R, r, and d, you can create a variety of intricate patterns and captivating designs in your artwork.

Trefoil Knot

The trefoil knot is a simple, non-trivial knot that creates a continuous loop with three crossings.

Equation: x(t) = (2 + cos(3 * t)) * cos(2 * t) y(t) = (2 + cos(3 * t)) * sin(2 * t) z(t) = sin(3 * t)

Parameters: t: The parameter that ranges from 0 to 2π.

Spirograph

The spirograph creates captivating, intricate, and looping patterns reminiscent of the classic drawing toy.

Equation: x(t) = (R - r) * cos(t) + p * cos(((R - r) / r) * t) y(t) = (R - r) * sin(t) - p * sin(((R - r) / r) * t)

Parameters: R: The radius of the larger circle. r: The radius of the smaller circle. p: The distance from the center of the smaller circle to the point tracing the curve. t: The parameter that ranges from 0 to 2π.

Fermat's Spiral: 

Fermat's spiral is a beautiful pattern resembling a double-arm spiral and is named after the French mathematician Pierre de Fermat.

Equation: x(t) = sqrt(t) * cos(t) y(t) = sqrt(t) * sin(t)

Parameters: t: The parameter that ranges from 0 to a specified value depending on the desired extent of the spiral.

Star Polygon

The star polygon creates a star-like shape with a customizable number of points and interconnections.

Equation: x(t) = cos(n * t) * cos(t) y(t) = cos(n * t) * sin(t)

Parameters: n: The number of points in the star polygon. t: The parameter that ranges from 0 to 2π

Cassini Oval

The Cassini oval creates a closed, oval-like curve defined by the fixed distance between two foci.

Equation: x(t) = a * cos(t) * sqrt(1 + (sin^2(t) * (b^2 - a^2) / a^2)) y(t) = b * sin(t) * sqrt(1 + (cos^2(t) * (a^2 - b^2) / b^2))

Parameters: a: The semi-major axis (half the width) of the oval. b: The semi-minor axis (half the height) of the oval. t: The parameter that ranges from 0 to 2π.

Vary the parameters of each equation to create a wide variety of captivating designs in your parametric art.

Figure-Eight Curve (Lemniscate of Gerono)

The Figure-Eight Curve creates a shape resembling the number eight or an infinity symbol.

Equation: x(t) = cos(t) y(t) = sin(2 * t) / 2

Parameters: t: The parameter that ranges from 0 to 2π.

Cardioid

The cardioid is a heart-shaped curve that can add a sense of love and warmth to your artwork.

Equation: x(t) = (1 - cos(t)) * cos(t) y(t) = (1 - cos(t)) * sin(t)

Parameters: t: The parameter that ranges from 0 to 2π.

Deltoid Curve

The deltoid curve creates a rounded, triangular shape similar to the deltoid muscle.

Equation: x(t) = 2 * cos(t) + cos(2 * t) y(t) = 2 * sin(t) - sin(2 * t)

Parameters: t: The parameter that ranges from 0 to 2π.

Clothoid

The clothoid, also known as the Euler spiral, is a curve that changes its curvature linearly with its curve length, creating smooth transitions in your artwork.

Equation: x(t) = integral[0 to t] (cos(s^2) ds) y(t) = integral[0 to t] (sin(s^2) ds)

Parameters: t: The parameter that ranges from 0 to a specified value depending on the desired extent of the clothoid.

Lissajous Bowtie

The Lissajous Bowtie is a variation of the Lissajous curve that creates a bowtie-like pattern.

Equation: x(t) = sin(a * t + δ) y(t) = sin(b * t)

Parameters: a: The frequency of the oscillation in the x-direction. b: The frequency of the oscillation in the y-direction. δ: The phase difference between the two oscillations. t: The parameter that ranges from 0 to 2π.

Vary the parameters of each equation to create a diverse array of captivating designs in your parametric art.